
The moments and product of inertia with respect to the x and y axes are Ix = 7.24x106 mm 4, I y = 2.61x106 mm 4, and Ixy = -2.54x106 mm 4. 9.25) and the principal moments of inertia (Eq.
Compute the product of inertia with respect to the xyaxes by dividing the section into three rectangles and applying the parallel axis theorem to each.Mohr’s circle may be used to graphically or analytically determine the moments and product of inertia for any other rectangular axes including the principal axes and principal moments and products of inertia.įor the section shown, the moments of inertia with respect to the xand yaxes are I x= 10.38 in4and I y= 6.97 in4.ĭetermine (a) the orientation of the principal axes of the section about O,and (b) the values of the principal moments of inertia about O.The moments and product of inertia for an area are plotted as shown and used to construct Mohr’s circle,.Mohr’s Circle for Moments and Products of Inertia I max and I min are the principal moments of inertia of the area about O.The equation for qm defines two angles, 90o apart which correspond to the principal axes of the area about O.At the points A and B, Ix’y’ = 0 and I x’ is a maximum and minimum, respectively.10-9a and 10-9c and adding, it is found that You need to use little wedge shapes pieces.Principal Axes and Principal Moments of Inertia Even as you make them infinitesimally thin this fails. Put another way, take a bunch of long thin rectangles of the same size cut out of paper and try to arrange them into an approximate segment of a circle without overlapping them. But looking at the diagram, clearly surface elements close to the origin need to be smaller than ones further away, otherwise you end up "overcounting" area near $r=0$ and under-counting area further out. So why doesn't your integral using a line work? Well, this treats surface elements at all distances from the origin as having the same size (I'm speaking very loosely here, since infinitesimals don't really have a size).

It follows that the width of the surface element is $r\ d\theta$ (the angle shrinks to an infinitesimal, but the radial coordinate does not - it simply takes the value of the radius wherever we place our surface element). It should be easy to convince yourself that the length of an arc that spans angle $theta$ is $r\theta$ (of course $theta$ in radians). But the length of the arc between two evenly spaced blue lines clearly increases as the radial coordinate increases.
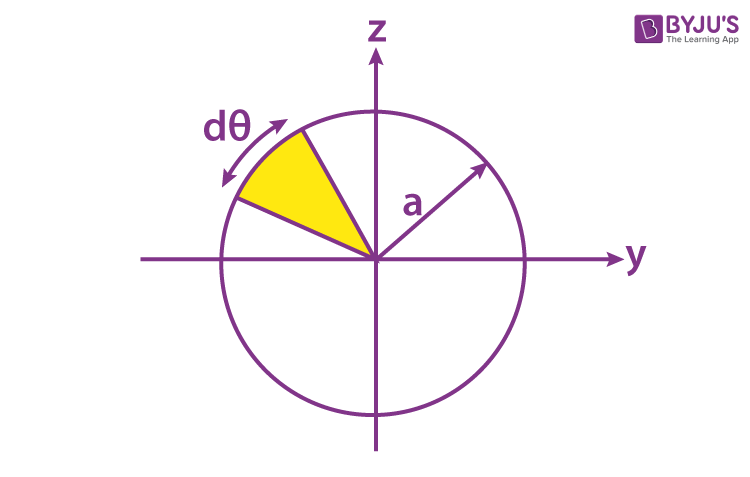
We don't need to worry about this because in the infinitesimal limit, they approach the same length.

First, you might notice that the "inner width" and "outer width" are different. The length is easy, it is $dr$, and is always the same (notice that the length of a blue segment between the evenly spaced red lines is always the same). In the infinitesimal limit the area of one such segment is just its length multiplied by its width. The surface element has the same shape as one of the spaces between two red and two blue lines (a sort of curved rectangle). The reason for this can be seen geometrically: When integrating in (2D) polar coordinates you need to use a surface element:


 0 kommentar(er)
0 kommentar(er)
